这就是来自马克斯·普朗克研究所等机构发表的工作:利用宇宙学和红移依赖性对宇宙结构形成进行场级仿真。
AI终于开始模拟宇宙了!LeCun也在第一时间转发和推荐:

作者表示:我们现在可以使用人工智能在多个时间步上对大多数宇宙学特性生成宇宙的冷暗物质模拟。
并且,物理学是这个神经网络设计的核心,它可以看成是PINN(内嵌物理知识神经网络)的一种实现,其损失函数建模了时间相关的粒子坐标和速度之间的特定关系。
在这项工作中,研究人员提出了一个用于大规模结构的场级模拟器,捕获宇宙学依赖性和宇宙结构形成的时间演化。
模拟器将线性位移场映射到特定红移处对应的非线性位移。
模拟器是一个神经网络,包含对Ω和红移z处的线性增长因子D(z)的依赖性进行编码的样式参数。

研究人员在六维N-body相空间上训练模型,将粒子速度预测为模型位移输出的时间导数,显著提高了训练效率和模型准确性。
最终,模拟器在测试数据(训练期间未见过的各种宇宙学和红移)上实现了良好的精度和性能,在z = 0,k ∼ 1 Mpc/h的尺度上达到了百分比级精度,并在较高红移下提高了性能。
通过合并树将预测的结构形成历史与N体模拟进行比较,可以找到一致的合并事件序列和统计特性。

并且,该模拟器速度极快,在单个GPU上半秒内就能够预测128的立方个粒子的非线性位移和速度场。
同时又可以通过多GPU并行处理进行良好的扩展,支持任意大尺寸的实现。
模拟宇宙的AI

比如利用N点统计的传统分析方法,需要大量模拟数据集来进行准确的协方差估计。
而基于模拟的推理方法和场级分析,则需要生成许多后期密度场的准确实现,以约束模型参数和初始条件重建。

DESI、Euclid、Vera C. Rubin天文台、SPHEREx和Subaru Prime Focus Spectrograph可以为研究者提供大量最新的星系巡天数据。
为了探明宇宙学参数和初始条件的最佳约束,需要对巡天观测值进行快速、高度准确的预测。
在这项工作中,作者通过添加红移依赖性和对多个红移模拟快照的训练来扩展场级N体模拟器。
由于本模型的时间依赖性和自可微性,研究者可以有效地获得N体粒子速度作为输出粒子位移的时间导数。
可以在训练期间动态评估这些速度,由此定义一个取决于粒子位置和速度的损失函数,在六维N体相空间上进行训练。
强制执行「速度必须等于位移时间导数」的物理约束,可以提高训练效率并提高模型的准确性,特别是对于速度场。
模型结构
作者通过周期模拟框中的坐标x来描述N体粒子。每个粒子都与规则立方晶格上的一个位点q相关联,因此它在红移z处的位置定义为:
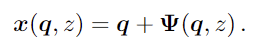
这里Ψ是位移场,q是粒子的拉格朗日坐标。在线性Zeldovich近似 (ZA) 中,位移场演变为:
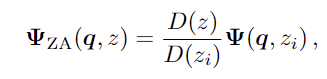
其中 D(z) 是线性增长因子,zi是早期选择的红移,以便线性理论可以很好地描述位移场。
随着引力簇的非线性在后期变得重要,这种线性近似变得不准确,而模拟宇宙结构形成的非微扰方法(如N体模拟)变得必要:
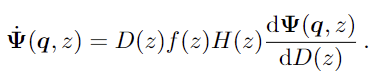
这里f(z)为线性增长率,H(z) 是哈勃率(Hubble rate),使用粒子速度来模拟星系探测中的红移空间扭曲。
研究人员设计了场级模拟器,根据目标红移处的ZA位移场来预测z = 3-0范围内任何红移处的非线性粒子位移和速度。
场级模拟器采用U-Net/V-Net设计,使用PyTorch的map2map库实现和训练模型。
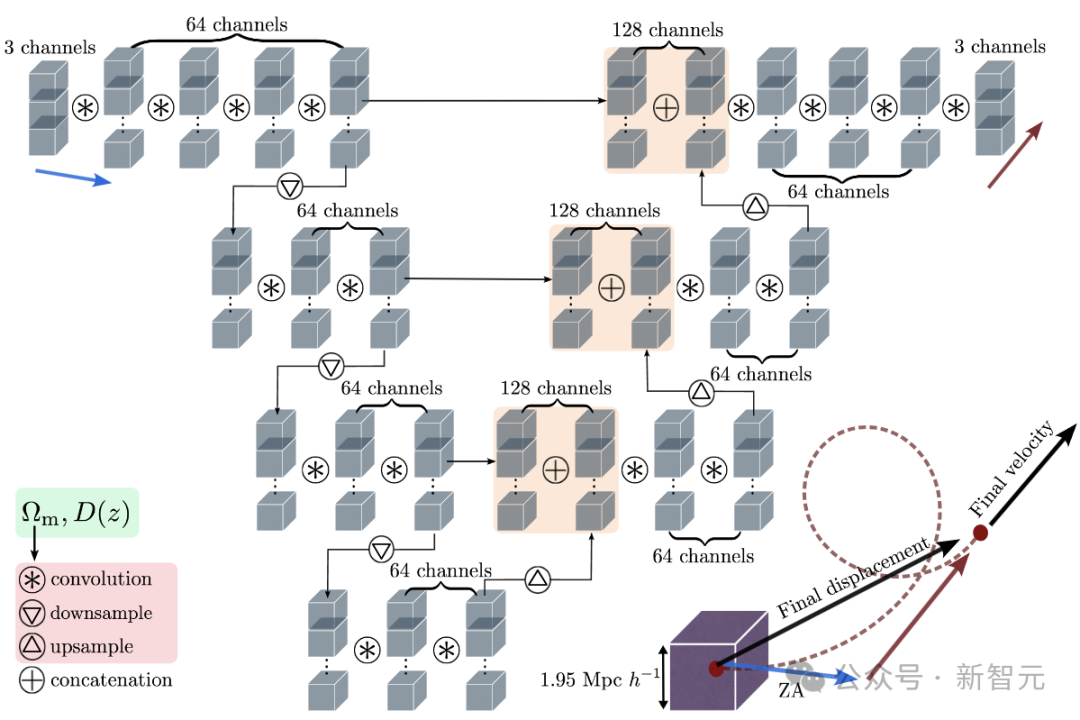
如上图所示,模型的输入具有三个通道,对应于所需红移处ZA位移的笛卡尔分量,排列在3D网格中。
输入经过四个ResNet 3×3×3卷积,第一个卷积运算将3个输入通道转换为64个内部通道。
在四次卷积操作之后,结果的副本被存储以供网络的上采样端使用,然后使用2×2×2卷积核对结果进行下采样。
该架构的感受野对应于给定焦点单元两侧的48个网格点。预测单个粒子的位移时,以焦点粒子为中心的大小为97的区域需要通过网络,对应于拉格朗日体积189.45 Mpc/h。
不过,由于网络缺少填充区域中所有单元的信息,因此这些区域的粒子位移并不准确,需要从输出中移除。
网络有限的感受野也有一个优点:它在线性理论准确的大尺度上保留了ZA场。
以上的操作可以针对固定宇宙学的单个红移来训练来自模拟快照的数据。
为了扩展网络功能,允许网络学习N体映射作为Ω和红移的函数,作者对其进行了增强以包含样式参数 。
在执行任何卷积(包括下采样/上采样操作)之前,快照的Ω和D(z)值将传递并映射到与卷积核尺寸匹配的内部数组,然后使用这些参数调节网络权重。
模型训练
训练数据
研究人员从一组具有不同宇宙学参数和一组固定快照红移的模拟中随机采样快照,同时训练样式参数和网络参数,使用Quijote Latin超立方体模拟,在边长1 Gpc/h的空间中使用512个粒子运行。
所有这些模拟的拉格朗日空间分辨率均为1.95 Mpc/h,整个数据集包含2000个模拟,每个模拟都有一组独特的五个ΛCDM宇宙学参数Ω。
研究人员将2000个模拟分为三组:1874个用于训练,122个用于验证,4个用于测试。为了鼓励各向同性,这里使用数据增强,通过立方体的对称性随机变换输入和目标数据。
损失函数
模型训练使用的损失函数包含四个项。第一个是粒子位移的平均平方误差(MSE),比较粒子的模拟器位移预测和真实的N体位移:
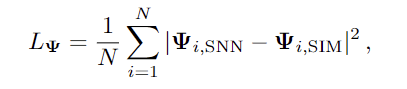
第二项是欧拉密度的MSE:
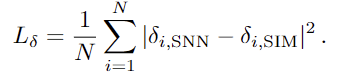
第三项是采用粒子速度的MSE:
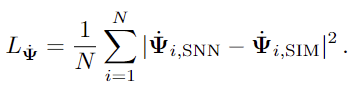
最后一项对应于欧拉动量场的MSE损失。这里将粒子速度分布到与初始拉格朗日网格具有相同分辨率的欧拉矢量场网格并计算,p是网格单元中每粒子质量的欧拉动量。
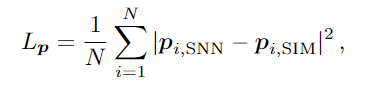
于是,红移z处快照的最终损失函数为:
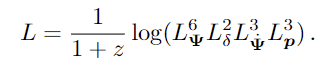
实验结果
研究人员通过构建模拟器输出和N体模拟真值的欧拉密度、和动量自功率谱和互功率谱来评估模拟器的准确性。
对于密度场,使用CIC插值方案将粒子分布到512网格并估计功率谱,下表列出了用于测试本文模拟器的五个模拟宇宙学参数:
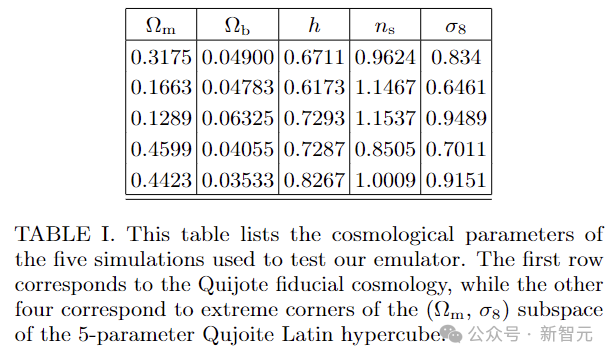
模拟器在训练过程中从未遇到过以上5种测试模拟中的任何一种。
下面测试在训练数据中的五个固定红移之间进行插值时的模型性能:
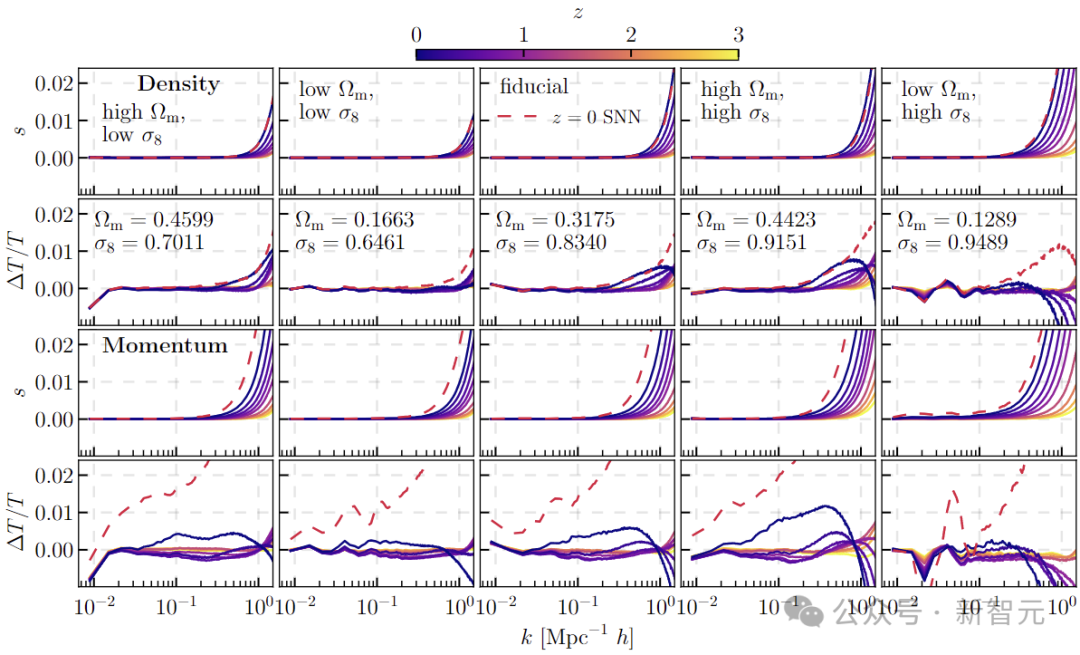
上图显示了SNN模拟器的功率谱误差(比例函数),每条曲线的颜色表示红移。
欧拉密度误差仅源于粒子位移的误差,当红移z = 0时,新的瞬态模型的随机性与原始模型的随机性相当,并且传递函数误差通常比原始模型有所改善。
在上图的最右列中,可以看到由于模拟器无法完美预测BAO幅度而导致的振荡误差。不过模拟器的这些错误特征低于1%,并且可能会随着更多的训练数据而得到改善。
红移相关模型的性能与z = 0时的真实空间密度统计数据相当,并且在较高红移时对于红移空间和真实空间统计数据的性能明显更好。
随着红移的减小,误差平滑且单调地增加。这表明模拟器可以在其训练数据中的少量固定红移快照之间有效地进行插值,而不会过度拟合,否则我们会在中间看到错误的振荡特征。


